อัตราส่วนที่เท่ากัน
ให้นักเรียนพิจารณาข้อความต่อไปนี้
แม่ให้รุ้งไปซื้อมะนาวจากตลาดข้างบ้าน รุ้งซื้อมะนาวมา 4 ผล ราคา 5 บาท จากข้อความดังกล่าว
สามารถนำมาเขียนในรูปอัตราส่วน เป็น 4:5
นักเรียนคิดว่า ถ้ารุ้งต้องการซื้อมะนาวตามจำนวนที่กำหนดในตาราง แล้วราคามะนาวจะเป็นเท่าไร
ให้นักเรียนเติมราคามะนาวในตารางให้สมบูรณ์
นักเรียนคิดว่าจะเขียนอัตราส่วนของจำนวนมะนาวเป็นผลต่อราคาเป็นบาทได้อย่างไรบ้าง ซึ่งคำ
ตอบจะเป็น ดังนี้
4:5 หรือ 8:10 หรือ 12:15 หรือ 16:20 หรือ 20:25
จะเห็นได้ว่าอัตราส่วนเหล่านี้ ได้มาจากการซื้อมะนาวในราคาเดียวกันคือ มะนาว 4 ผล ราคา 5 บาท
และกล่าวว่าอัตราส่วนเหล่านั้นเป็น อัตราส่วนที่เท่ากัน ซึ่งเขียนได้ ดังนี้
4:5 = 8:10 = 12:15 = 16:20 = 20:25
หรือ 4 = 8 = 12 =16 = 20 เราจะสังเกตเห็นว่า อัตราส่วนที่เท่ากันข้างต้นมีความเกี่ยวข้องกับอัตราส่วน
5 10 15 20 25
4 ดังนี้
5
การทำอัตราส่วนให้เท่ากับอัตราส่วนที่กำหนดไว้ข้างต้น เป็นไปตามหลักการหาอัตรา
ส่วนที่เท่ากัน ดังนี้
หลักการคูณ เมื่อคูณแต่ละจำนวนในอัตราส่วนใดด้วยจำนวนเดียวกันโดยที่จำนวน
นั้นไม่เท่ากับศูนย์ จะได้อัตราส่วนใหม่ที่เท่ากับอัตราส่วนเดิม
หลักการหาร เมื่อหารแต่ละจำนวนในอัตราส่วนใดด้วยจำนวนเดียวกันโดยที่จำนวน
นั้นไม่เท่ากับศูนย์ จะได้อัตราส่วนใหม่ที่เท่ากับอัตราส่วนเดิม
ตัวอย่างที่ 1 จงหาอัตราส่วนที่เท่ากับอัตราส่วน 7:9 มาอีก 2 อัตราส่วนโดยใช้หลักการคูณวิธีทำ
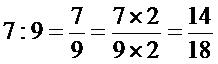
ดังนั้น อัตราส่วนที่เท่ากับอัตราส่วน 7:9 คือ 14:18 และ 21:27
ตัวอย่างที่ 2 จงหาอัตราส่วนที่เท่ากับอัตราส่วน 122 มาอีก อัตราส่วนโดยใช้หลักการหาร
180
วิธีทำ
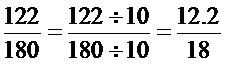
ดังนั้น อัตราส่วนที่เท่ากับอัตราส่วน 122 คือ 61 และ 12.2
180 90 18
ตอบ 61 และ 12.2
90 18
ตัวอย่างที่ 3 ร้านค้าแห่งหนึ่งขายปากกาในราคาโหลละ 36 บาท ราณีต้องการซื้อปากกา 60 ด้าม
ราณีต้องจ่ายเงินเท่าไร สมัยต้องการซื้อปากกาในราคาเดียวกันนี้บ้าง แต่มีเงินเพียง 6 บาท ถ้าร้านค้า
ยอมขายปลีกให้ในราคาเดียวกัน สมัยจะซื้อปากกาได้กี่ด้าม
วิธีทำ ร้านค้าขายปากกาในราคาโหลละ 36 บาทเขียนอัตราส่วนของจำนวนปากกาเป็นด้ามต่อราคา
เป็นบาท เป็น 12
36
ต้องการซื้อ 60 ด้าม จึงต้องทำจำนวนแรกของอัตราส่วนให้เป็น 60 ซึ่งเท่ากับ 12×5
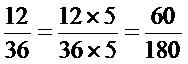
ดังนั้น ราณีต้องจ่ายเงิน 180 บาท
สมัยต้องการซื้อปากกาในราคาเดียวกับราณี แต่มีเงินเพียง 6 บาท
มีเงิน 6 บาท จึงต้องทำจำนวนหลังของอัตราส่วนให้เป็น 6 ซึ่งเท่ากับ
ดังนั้น สมัยซื้อปากกาได้ 2 ด้าม
ตอบ ราณีจ่ายเงิน 180 บาท , สมัยซื้อปากกาได้ 2 ด้าม
หมายเหตุ มีอัตราส่วนบางอัตราส่วนที่เราไม่สามารถนำอัตราส่วนที่เท่ากับอัตราส่วนนั้น
มาใช้ เพราะเมื่อนำมาใช้แล้วจะทำให้ความหมายผิดไป เช่น จากข้อความ “ภราดร แข่ง
ขันเทนนิสชนะ 3 ต่อ 2 เซท” เมื่อนำมาเขียนในรูปอัตราส่วน จะได้ ดังนี้
อัตราส่วนของจำนวนเซทที่ภราดร ชนะต่อจำนวนเซทที่ภราดรแพ้เป็น 3:2 ซึ่ง
หมายความว่าในการแข่งขันเทนนิส 5 เซท ภราดรชนะ 3 เซท และแพ้ 2 เซท
ถ้าเราหาอัตราส่วนที่เท่ากับ 3:2 ได้เป็น 6:4 ก็ไม่ได้หมายความว่า ในการแข่งขันเทนนิส
10 เซท ภราดรจะต้องชนะ 6 เซท และแพ้ 4 เซท
การตรวจสอบการเท่ากันของอัตราส่วนโดยใช้การคูณไขว้
พิจารณาอัตราส่วนสองอัตราส่วนต่อไปนี้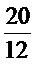
กับ 
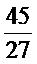
เราสามารถตรวจสอบว่า อัตราส่วนทั้งสองนี้เท่ากับหรือไม่ ดังนี้
จำนวน 27 ที่นำมาคูณเป็นจำนวนหลังของอัตราส่วน
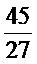และ
จำนวน 12 ที่นำมาคูณเป็นจำนวนหลังของอัตราส่วน
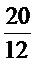และ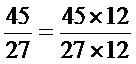 
เนื่องจาก 12×27 = 27×12
จึงตรวจสอบว่า 20×27 = 45×12 หรือไม่
เนื่องจาก 20×27 = 540 และ 45×12 = 540
ดังนั้น 20×27 = 45×12
จึงสรุปได้ว่า
กับ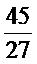 
เป็นอัตราส่วนที่เท่ากันให้สังเกตว่า 20×27 และ 45×12 ได้มาจากการคูณไขว้ ดังแผนภาพ
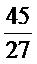
ซึ่ง ผลคูณไขว้ 20×27 = 45×12 ข้างต้นนี้ ทำให้เราสรุปได้ว่า อัตราส่วน
และ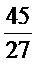 
เท่ากันโดยทั่วไปเราสามารถตรวจสอบการเท่ากันของอัตราส่วน
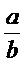และ 
ด้วยการ คูณไขว้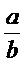 
แล้วพิจารณา ผลคูณไขว้ a x d และ b x c ตามหลักการ ดังนี้
ถ้า a x d = b x c แล้ว
= 
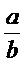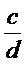
ถ้า a x d
b x c แล้ว 
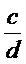
จากหลักการข้างต้น ทำให้ได้ข้อสรุปต่อไปอีกว่า
ถ้า
= 
แล้ว a x d = b x cตัวอย่างที่ 4 จงตรวจสอบว่าอัตราส่วนในแต่ละข้อต่อไปนี้เท่ากันหรือไม่
1)
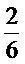และ 
2)
และ 
วิธีทำ 1) จากการคูณไขว้
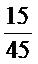
จะได้ 2×45 = 90
6×15 = 90
ดังนั้น 2×45 = 6×15
นั่นคือ
= 
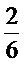2) จากการคูณไขว้
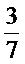
จะได้ 3×10 = 30
7×6 = 42
ดังนั้น 3×10
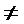7×6นั่นคือ
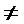
ตอบ 1)
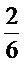และ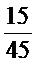
เป็นอัตราส่วนที่เท่ากัน2)
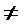
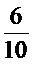เป็นอัตราส่วนที่ไม่เท่ากัน
ไม่มีความคิดเห็น:
แสดงความคิดเห็น